MT-SLVR: Co-Learning Towards Harmony in Audio Processing
Published:
‘MT-SLVR: Multi-Task Self-Supervised Learning for Transformation In(Variant) Representations’ was released in late May 2023, after being accepted to InterSpeech23. It proposed a novel multi-task learning approach, capable of co-learning seemingly conflicting features. This blog aims to be a more informal and digestible breakdown of the work. All relevant code, or links to, can be found here.

Motivation & Aims
Contrastive learning algorithms (as discussed in more detail later on) have seen remarkable successes in recent years as a method of self-supervised pre-training. One possible explanation for this success is that they learn implicit augmentation invariance, which on many downstream testing benchmarks is beneficial. We, as well as a small handful of other works, suggest that although this invariance may be helpful in specific cases, it is likely not helpful in all.
We pose this hypothesis along with an example: Assuming that we have trained a contrastive model which has implicitly learned to be rotationally invariant, we would possibly expect strong performance on a task like object detection (where rotation is mostly irrelevant - an object is most likely the same regardless of orientation). Using the same model for a task like pose detection however would likely result in poor performance, due to the dependence on rotation features for distinguishing between actions such as standing or lying down. This entire example can be reversed for predictive based methods, where we likely learn a degree of augmentation invariance or sensitivity.
We use this insight as motivation, and set out the following research question: Is it possible to co-learn both augmentation invariant and equivariant features? If so, does having access to both increase average downstream task performance.
Self-Supervised Learning
Self-supervised learning has seen massive success in past years, even beating traditional supervised approaches in certain tasks. The most influential approaches belonging to this family make heavy use of augmentation pipelines in order to help define their pre-text task. For example, a simple approach may be to rotate images and then predict their rotation. This is a just simple example and is not state-of-the-art , but it gives an idea of how known changes to data can be used to define an objective.
Within these types of augmentation based approaches, there are generally two categories, Predictive and Contrastive
Predictive Learning
Predictive approaches are those which predict some information about the augmentations being used in the pipeline, the example given earlier fits into this. Other variants of this can easily be defined, however as they are generally less popular within current literature, there exists no systematic analysis of how they compare with respect to learns sensitivity/equivariance or downstream performance.
Contrastive Learning
Contrastive approaches can be though of as the opposite of predictive approaches (although exactly how they function makes that comparison more difficult to see). One of the most successful contrastive algorithms introduced is SimCLR, which effectively uses augmentations to define classes. Without going into too much detail here, SimCLR effectively takes every sample in a given batch and augments it in two unique ways (called views), for each sample these views are then considered a class, meaning that each batch of N samples, effectively becomes a batch of N classes. This setup can then be used along with a modified variant of cross-entropy in order to learn a model. Although it is generally a much less obvious example than the predictive case, the SimCLR approach described above effectively learns to ignore the augmentations used due to how classes are created.
MT-SLVR
On the surface, trying to learn both contrastive and predictive feature representations within a single model seems ill-posed, how can it be possible to learn both invariance and equivariance?! Turns out it is possible, but requires a few additional considerations in order to get there.

Basis of Algorithm
We form the basis of our approach on adapters, effectively small parametrised modules that can be included through a larger model. Introduced most notably in this work, multiple adapters can be used in order to learn specific features for tasks while sharing the majority of parameters. This is kind of our silver bullet for MT-SLVR, by using adapters we were able to somewhat localise both predictive and contrastive specific features, while sharing the vast majorly of parameters.

Audio Augmentations & Application
We utilise the augmentations (and their respective parameter options) as proposed by the work “Contrastive Learning for Auditory Representations” (CLAR). In total, this covers 7 possible augmentations, each with some parameter space to sample from.
| Augmentation | Shorthand | Parameter | Value(s) |
|---|---|---|---|
| Pitch Shift | PS | Min / Max Transpose Semitones | -15 / 15 |
| Shape | Lin, Log, Exp | ||
| Fade | FD | Max In / Out Ratio | 0.5 / 0.5 |
| Min / Max SNR in dB | 3 / 30 | ||
| White Noise | WN | Min Max f-Decay | -1 / 0 |
| Min / Max SNR in dB | 3 / 30 | ||
| Mixed Noise | MN | Min Max f-Decay | -2 / 2 |
| Time Masking | TM | Max Mask Ratio | 0.125 |
| Time Shift | TS$^1$ | Min / Max Shift Ratio | 0.5 |
| Time Stretch | TS$^2$ | Min / Max Stretch Factor | 0.5 / 1.5 |
At sampling and application time, given a new un-augmented sample x, we follow this process:
- Choose num (between 1 and 7) of the possible augmentations to use
- Randomise the order which they are applied
- Randomly sample 2 sets of parameters for the whole augmentation pipeline, i.e if the pipeline is [pitch shit -> white noise -> fade], we want to sample two variants of this pipeline (same augmentations and same order) with different parameters. This creation of two connected augmented pipelines is necessary for the contrastive learning part of our algorithm
- Pass our original sample x through each pipeline separately, creating two unique samples (two unique views as called in original SimCLR work)
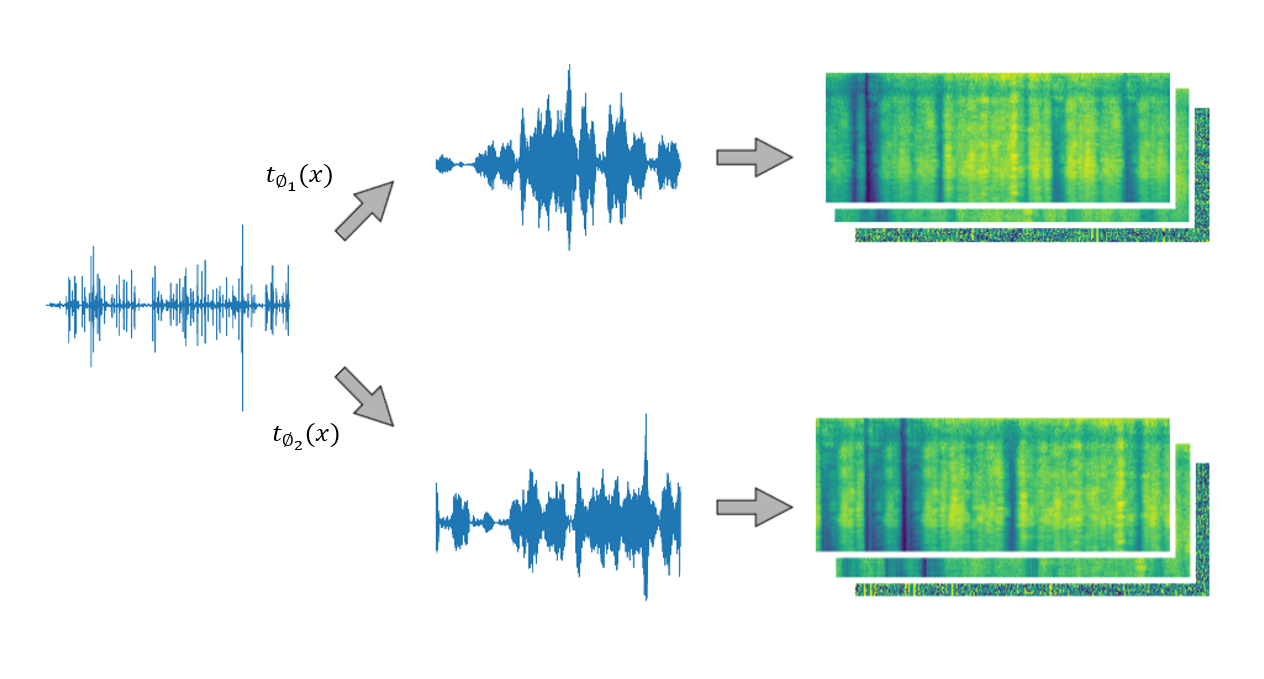 Figure 3: Example contrastive augmentation pipeline. The augmentation operators consist of the same type of augmentations in the same order, but differ in parameters.
Figure 3: Example contrastive augmentation pipeline. The augmentation operators consist of the same type of augmentations in the same order, but differ in parameters.
Processing & Input
After augmentations have been applied, we follow a combination of the processes outlined in MetaAudio and the CLAR work. Each sample is first z-normalised and later converted to a 3-channel 2-dimensional input. Details on the input size (i.e 3-channel 2-dim) are best found here our 1-d audio sample into a 3-channel Mel-spectrogram.
Model Variants
In order to effectively test this idea that we can retain some lightweight task specific parameters, we consider a variety of versions of MT-SLVR. Specifically we consider 5 versions:
- A naïve approach where there are no task specific parameters for either constrictive or predictive objectives, The objectives are forced to share every parameter in the backbone model
- A split head approach, where the only task specific parameters allowed to either objective is half of the final output layer neurons, i.e for an 1000 total output dim fully connected layer, we split it into two heads of 500, one which is only used for contrastive and one which is only used for predictive. This split head is also used in the variants which employ adapters
- Split head and adapter approaches with 3 different type of adapters: Batch Norm, Series and Parallel - all can be found in the original residual adapters work here
Training Pipeline
The MT-SLVR training pipeline can be summarised as follows:
- Grab a batch of some N samples from our dataset
- Generate augmentation pipelines (as discussed in section above)
- Make a note of the augmentations applied to each sample, this can be used later for the predictive part of our approach
- Create our augmented batch: Each original sample has now been transformed into 2 distinct but correlated views
- Pass our augmented batch through the model in two separate ways:
- Once through the shared encoder and the contrastive specific parameters and head
- Once through the shared encoder and the predictive specific parameters and head
- Calculate the contrastive and predictive losses separately using their respective objective functions
- Combine the losses in some way (we use simple weighted average)
- Backpropagate joint loss to update the model
Evaluation Pipeline
At evaluation time (once the trained model is frozen), we generate feature representations of new samples by doing the following:
- Processing the new input sample in the same way as our training data, but with no application of augmentations
- Pass the new sample through the model:
- One pass through which uses the shared and contrastive parameters
- Another pass through (starting form original sample)which uses the shared and predictive parameters
- Should now have two sets of features for our 1 input sample. One set of contrastive and one set of predictive
- For our downstream experiments, we concatenated our feature sets for use
Few-Shot Audio Classification
For evaluation we use few-shot audio classification (a task described more in the MetaAudio blog post). Overall our evaluation process is similar to that described in MetaAudio with respect to how tasks are sampled and how variable length sets are treated.

This being said, our works evaluation pipeline and methodology are distinct in that we do self-supervised pre-train on a separate dataset and then use linear readout for our downstream tasks, effectively assuming no knowledge of them nor doing any fine-tuning.
In more detail: We are not doing any kind of training with the datasets which we are later evaluating on (distinct to meta-learning covered in MetaAudio which does this). We pre-train our models on a generic audio dataset (balanced AudioSet), and then freeze their parameters entirely (no updates at all based on downstream tasks) in order to use it as a static encoder, which can be used to generate feature representations for incoming few-shot tasks (which can then be later solved by some classifier using the feature representations).
Data, Backbone | Setup
Datasets
We train all of our models with the balanced train split of AudioSet. Although this set fit perfectly for our needs with respect to size and convienece, we acknowledge that it is not perfectly reproducible, and so we we plan on updating our work in some way to rectify this issue.
| Name | Setting | No. Classes | No. Samples | Format | Sample Length |
|---|---|---|---|---|---|
| Balanced AudioSet | Mixed | 527 | 20,550 | Fixed | 10s |
| ESC-50 | Environmental | 50 | 2,000 | Fixed | 5s |
| NSynth | Instrumentation | 1,006 | 305,978 | Fixed | 4s |
| FDSKaggle18 | Mixed | 41 | 11,073 | Variable | 0.3s - 30s |
| Watkins Marine Mammal Sounds | Marine Mammals | 32 | 1,698 | Variable | 0.1 - 150s |
| BirdCLEF 2020 (Pruned) | Bird Song | 715 | 63,364 | Variable | 3s - 180s |
| VoxCeleb1 | Speaker | 1,251 | 153,516 | Variable | 3s - 180s |
| SpeechCommandsV2 | Keyword | 35 | 105,829 | Fixed | 1s |
| Crema-D | Emotion | 6 | 7,442 | Variable | 1s - 5s |
| Speech Accent Archive | Accent | 122 | 2,060 | Variable | 17s - 110s |
| Common Voice v12 Delta | Language | 88 | 256,243 | Variable | 5s - 30s |
For evaluation we consider a wide variety of datasets. The majority of these come from our original MetaAudio work (still using the same tets split so are comparable) however we supplemented our set of tasks by sourcing some speech focused sets. More specifically, we found, formatted and made few-shot testing sets out of:
- Speech Accent Archive: English speech spoken by non-native speakers. Accent classification
- Crema-D: Emotion classification
- Common Voice: We used the delta v13 release. Language classification
With these additions, the 10 total sets can be split into: 5 environmental/animal sound based datasets, and 5 speech based datasets.
Main Experiments & Results
We directly tested the effectiveness of our novel approach by comparing it and its variants against both contrastive and predictive only baselines. For our contrastive learning objectives we conducted experiments with both SimCLR and SimSiam (details of both approaches can be found in their respective original papers). For predictive learning we utilised a multi-label augmentation detection objective (effectively a multi-label classification over augmentations, where a label of 1 is assigned if that augmentation is present and 0 otherwise).
5-Way 1-Shot Performance Comparison between SimCLR methods. We compare SimCLR on its own (Baseline), Multi-Task Learning with no, or simple tricks (MT-Simple / Split), and Multi-Task with adapters (MT-Bn / Series / Parallel)
| Model ($f_\theta$) | ESC-50 | NSynth | Kaggle18 | Watkins | BirdClef | VoxCeleb | SCv2 | Crema-D | SAA | C-Voice | Avg Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cont Only | 63.40 ± 0.39 | 66.44 ± 0.40 | 37.64 ± 0.40 | 52.91 ± 0.41 | 30.93 ± 0.38 | 31.18 ± 0.37 | 25.68 ± 0.35 | 29.10 ± 0.36 | 26.16 ± 0.34 | 33.33 ± 0.38 | 3.9 |
| Pred Only | 37.76 ± 0.34 | 62.52 ± 0.36 | 21.72 ± 0.34 | 28.88 ± 0.39 | 21.04 ± 0.35 | 20.08 ± 0.37 | 23.40 ± 0.34 | 29.07 ± 0.37 | 26.27 ± 0.34 | 31.80 ± 0.37 | 7.0 |
| MT-Simple | 64.23 ± 0.39 | 66.73 ± 0.39 | 36.70 ± 0.40 | 55.26 ± 0.42 | 29.39 ± 0.37 | 30.91 ± 0.36 | 24.02 ± 0.34 | 29.07 ± 0.37 | 26.32 ± 0.34 | 33.21 ± 0.38 | 4.4 |
| MT-Split | 61.23 ± 0.39 | 65.29 ± 0.40 | 33.42 ± 0.38 | 53.19 ± 0.41 | 27.38 ± 0.36 | 29.71 ± 0.36 | 23.40 ± 0.34 | 28.66 ± 0.37 | 26.27 ± 0.34 | 31.80 ± 0.37 | 5.8 |
| MT-Bn | 69.17 ± 0.38 | 72.44 ± 0.39 | 39.11 ± 0.41 | 58.80 ± 0.43 | 30.32 ± 0.38 | 32.10 ± 0.38 | 24.40 ± 0.35 | 30.03 ± 0.38 | 28.61 ± 0.37 | 34.72 ± 0.40 | 2.1 |
| MT-Series | 69.00 ± 0.39 | 71.25 ± 0.39 | 37.28 ± 0.40 | 58.92 ± 0.42 | 28.82 ± 0.38 | 33.26 ± 0.38 | 24.66 ± 0.35 | 29.57 ±0.38 | 28.74 ± 0.37 | 34.23 ± 0.38 | 2.9 |
| MT-Parallel | 69.53 ± 0.39 | 71.81 ± 0.39 | 38.36 ± 0.40 | 59.49 ± 0.42 | 29.49 ± 0.38 | 33.58 ± 0.39 | 23.65 ± 0.34 | 29.61 ± 0.38 | 28.92 ± 0.37 | 35.22 ± 0.40 | 1.9 |
In total 8/10 of the best results for our downstream datasets are from Mt-SLVR based approaches, indicating a strong win for our MT-SLVR approach. This being said there is some scattering between the variants, with best results split between MT-BN and MT-Parallel. For the 2 datasets where our contrastive only baseline took the win, we note that the performance difference is much smaller than in cases where contrastive baseline lost, e.g. 1-2% compared to 5-6%.
5-Way 1-Shot Performance Comparison between SimSiam methods. We compare SimSiam on its own (Baseline), Multi-Task Learning with no, or simple tricks (MT-Simple / Split), and Multi-Task with adapters (MT-Bn / Series / Parallel)
| Model ($f_\theta$) | ESC-50 | NSynth | Kaggle18 | Watkins | BirdClef | VoxCeleb | SCv2 | Crema-D | SAA | C-Voice | Avg Rank |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cont Only | 51.74 ± 0.40 | 68.78 ± 0.39 | 31.72 ± 0.37 | 48.29 ± 0.42 | 23.94 ± 0.33 | 24.13 ± 0.32 | 23.80 ± 0.35 | 28.11 ± 0.32 | 23.51 ± 0.31 | 28.50 ± 0.36 | 5.0 |
| Pred Only | 37.76 ± 0.34 | 62.52 ± 0.36 | 21.72 ± 0.34 | 28.88 ± 0.39 | 21.04 ± 0.35 | 21.68 ± 0.40 | 20.08 ± 0.37 | 21.68 ± 0.33 | 23.08 ± 0.34 | 23.00 ± 0.42 | 7.0 |
| MT-Simple | 51.87 ± 0.40 | 69.68 ± 0.38 | 29.45 ± 0.36 | 53.13 ± 0.42 | 24.14 ± 0.34 | 25.84 ± 0.35 | 21.81 ± 0.33 | 26.42 ± 0.36 | 27.65 ± 0.35 | 28.96 ± 0.36 | 4.4 |
| MT-Split | 52.07 ± 0.40 | 68.26 ± 0.39 | 28.68 ± 0.36 | 52.04 ± 0.42 | 24.47 ± 0.34 | 25.58 ± 0.34 | 22.08 ± 0.33 | 26.69 ± 0.36 | 26.70 ± 0.35 | 28.58 ± 0.36 | 4.8 |
| MT-Bn | 58.41 ± 0.41 | 73.42 ± 0.38 | 31.69 ± 0.39 | 55.46 ± 0.43 | 25.44 ± 0.35 | 26.71 ± 0.36 | 21.99 ± 0.34 | 28.90 ± 0.37 | 27.38 ± 0.35 | 29.64 ± 0.37 | 3.0 |
| MT-Series | 57.24 ± 0.40 | 74.37 ± 0.37 | 37.31 ± 0.39 | 54.70 ± 0.42 | 25.20 ± 0.36 | 26.87 ± 0.36 | 22.64 ± 0.34 | 30.62 ± 0.37 | 26.44 ± 0.35 | 31.07 ± 0.38 | 2.7 |
| MT-Parallel | 60.61 ± 0.41 | 76.36 ± 0.37 | 37.59 ± 0.40 | 57.98 ± 0.42 | 25.45 ± 0.37 | 28.66 ± 0.34 | 23.08 ± 0.34 | 30.72 ± 0.37 | 27.94 ± 0.36 | 32.72 ± 0.72 | 1.1 |
The results for SimSiam based experiments are significantly more clear, with a total of 9/10 best results for our tasks coming from the parallel adapter variant of MT-SLVR. Similarity to what we identified for SimCLR, in the case where contrastive only won, the margin won by is much smaller than the reverse.
Across both SimSiam and SimCLR based experiments, we observe that both the simple and split head only variants of MT-SLVR perform similarity to (or worse) than the contrastive baseline. We hypothesise that this is due to lack of task specific parameters, either at all in the case of Mt-Simple, or throughout the entire model in the case of MT-Split. We propose that the key to effectively solving this co-learning problem between conflicting features lies in effective use of task specific parameters, where their inclusion prevents the model from being forced to encode both representations on top of one another.
We also note that predictive only baseline performed incredibly poorly, coming last in every single task. We don’t have a confident takeaway for this but one possible guess is that for these tasks to be successfully solved, features which have some level of invariance are required. This hypothesis may also be supported by the observation that the predictive baseline did best (with respect to relative difference in performance to other approaches) for NSynth, a dataset which consists of clean instrumentation, and may be more easily solved with knowledge of many of the specific augmentations included in our setup.
Ablation Studies
Learnt Invariance
To probe what invariance our frameworks learned, we measured the Mahalanobis distance between our original and augmented training samples.
Measured average Mahalanobis distance between original and augmented training (AudioSet) samples for SimCLR based models’ (P)redictive or (C)ontrastive heads. Lower values indicate more invariance to the transformation. Augmentations (in their shorthand) are given across the top row
| Model ($f_\theta$) | Head | PS | FD | WN | MN | TM | TS$^1$ | $TS^2$ | Avg |
|---|---|---|---|---|---|---|---|---|---|
| Cont Only | - | 32.01 | 31.23 | 31.67 | 31.66 | 30.96 | 31.61 | 31.35 | 31.5 |
| Pred Only | - | 38.17 | 40.81 | 41.26 | 40.73 | 54.21 | 30.39 | 43.83 | 41.34 |
| MT-Simple | - | 29.09 | 32.62 | 31.86 | 31.01 | 29.05 | 22.45 | 36.77 | 30.41 |
| MT-Split | C | 37.22 | 38.66 | 39.16 | 37.86 | 37.50 | 30.77 | 43.01 | 37.74 |
| P | 37.31 | 38.73 | 39.24 | 37.95 | 37.78 | 30.77 | 43.15 | 37.85 | |
| MT-Bn | C | 27.62 | 31.93 | 28.48 | 27.51 | 29.98 | 21.38 | 35.68 | 28.94 |
| P | 29.58 | 34.95 | 31.98 | 30.79 | 35.39 | 21.42 | 40.67 | 32.11 | |
| MT-Series | C | 22.71 | 26.16 | 23.38 | 23.15 | 21.00 | 21.33 | 30.24 | 24.00 |
| P | 36.59 | 37.71 | 39.09 | 38.78 | 44.44 | 21.28 | 42.12 | 37.14 | |
| MT-Parallel | C | 31.41 | 32.37 | 31.69 | 31.51 | 30.07 | 30.34 | 33.88 | 31.61 |
| P | 35.67 | 42.53 | 39.99 | 40.01 | 42.74 | 30.24 | 41.21 | 38.91 |
We observe a few interesting things:
- Our contrastive and predictive baselines behave as expected with respect to invariance, with the predictive baseline showing a much weaker invariance than its contrastive counterpart
- Different heads of our multi-task approaches do generally learn significantly different degrees of augmentation invariance to applied augmentations
- On average, even the simple multi-task approach decreases invariance compared to the contrastive only baseline
- MT-Split (our somewhat naïve approach to task specific parameters) does not successfully learn any difference in invariance strength between its different heads, a possible explication for its weaker relative performance
- We do not see a clear or consistent trend where the larger the difference of invariance strength between heads is predictive of final performance ranking
Feature Selection
As a final ablation, we examine average weight norms learned for each of the multi-task heads by our downstream linear classifiers. We do this for a representative selection of our evaluation datasets.
Average linear classifier feature weight for the (P)redictive and (C)ontrastive heads in multi-task SimCLR
| Model ($f_\theta$) | Head | ESC-50 | NSynth | BirdClef | Crema-D | SAA | C-Voice |
|---|---|---|---|---|---|---|---|
| MT-Split | C | 0.43 | 0.41 | 0.40 | 0.46 | 0.41 | 0.36 |
| P | 0.57 | 0.59 | 0.60 | 0.54 | 0.59 | 0.64 | |
| MT-Bn | C | 0.41 | 0.39 | 0.41 | 0.43 | 0.40 | 0.37 |
| P | 0.59 | 0.61 | 0.59 | 0.57 | 0.60 | 0.63 | |
| MT-Series | C | 0.39 | 0.33 | 0.36 | 0.39 | 0.37 | 0.30 |
| P | 0.61 | 0.67 | 0.64 | 0.61 | 0.63 | 0.70 | |
| MT-Parallel | C | 0.41 | 0.37 | 0.36 | 0.38 | 0.38 | 0.31 |
| P | 0.59 | 0.63 | 0.64 | 0.62 | 0.62 | 0.69 |
Generally we see that across different downstream tasks, the importance of contrastive vs predictive heads varies quite significantly. This suggests that depending on the task being solved there is a preference on what family of features to use. This nicely illustrates the benefits of our approach, in that we don’t rely on designing the perfect pre-tet task for our downstream problem, but instead learn more diverse features which can be sub-selected from.
Conclusion
In our work we demonstrated that it is indeed possible to co-learn features which are generally considered conflicting. We did this by making use of multi-task learning, with our major insight coming in the form of using adapters to provide some task specific parameters to our objectives. We evaluated our approach (a multiple variants of it) on a wide variety of downstream few-shot audio tasks, which generally showed that we best single objective baselines. These results were then follows up by some ablation studies, which suggested that our approach worked off of our hypothesis principle of augmentation invariance. We hope to extend this work in the future by considering a much wider and more granular experimental setup, hopefully allowing us to obtain some deeper insights into why this approach is so successful.
Thank you very much for Reading!
